昼間人口メッシュデータ
政府の統計に基づく日本全国の推計昼間人口メッシュデータを作りました。 令和2年国勢調査から算出した昼間常住人口に、令和3年の経済センサス・学校基本調査から推計した流入人口を加えたものです。
CSV形式の3次(1km)・4次(500m)・5次(250m)メッシュデータを無償で提供します。 情報源、加工手順、推計方法と問題点、精度も開示しています。 利用目的に適うか、下の記事を読んで判断してください。
目次
昼間人口とは
ある地域に住んでいる人々の数を、その地域の「常住人口」といいます。 通学・通勤のために、日々その地域から別の地域へ出たり、別の地域からその地域へ入ってきたりする人々の数を、「流出・流入人口」といいます(ここでは、買物・遊興・観光のような非定常的な移動は含まない)。
「常住人口 - 流出人口 + 流入人口」を、日中に社会活動している人々のイメージで「昼間人口」と呼びます。 これに対応して、常住人口を「夜間人口」とも呼びます。
昼間人口は、動的な状態とまではいえないものの、わたしたちの暮らす現実により近く、いわゆる商圏分析などの指標のひとつになります。 都市部では昼間人口が夜間人口より多く、郊外ではその逆になるといった傾向が、たとえ未知の地域でも数値からわかるのです。
有用な昼間人口データですが、これがメッシュデータであれば、さらにきめ細かな分析に役立ちます。 メッシュデータとは、対象の空間(地図)を、市区町村などの境界ではなく、均一な格子で網目状に区切ったデータです。
昼間人口のメッシュデータ
ありそうで無い
昼間人口を算出するために必要な流出・流入人口は、国勢調査でも把握されています。 「従業地または通学地」を回答した覚えのあるかたもいるでしょう。
しかし、その粒度は市区町村単位です。 これではメッシュデータになりません。
したがって、国勢調査をつかさどる総務省統計局においても、昼間人口のメッシュデータは、他のデータを組み合わせた推計によって作っていました。
「いました」と過去形で書いたのは、今はもう作られていないからです(『総務省統計局が作成した地域メッシュ統計の種類と結果資料(PDF)』)。 かつてのデータもウェブ上には見当たらず、あったとしてもデジタルメッシュマップなる形式はどうも機械可読ではなさそう。 推計だからと控えているのか事情は知りませんが、統計局は昼間人口メッシュには消極的に見受けられます。
あいまいな算出方法
せっかくノウハウがあるのにもったいない話です。 しかしないものはない以上、欲しければめいめいで作ってみるしかありません。 そのためにでもないでしょうが、統計局は算出式だけは次のように公表しています。
昼間人口の算出式
昼間人口 = 国勢調査 15歳以上非労働力人口
- 国勢調査 15歳以上通学者数
+ 国勢調査 未就学者数
+ 国勢調査 完全失業者数
+ 国勢調査 農林水産業就業者数
+ 事業所・企業統計調査 第2次産業事業所従業者数
+ 事業所・企業統計調査 第3次産業事業所従業者数
+ 通学地域メッシュ別生徒・学生数
(『総務省統計局における地域メッシュ統計の作成(PDF)』より)
この式も「常住人口 - 流出人口 + 流入人口」を意味していますが、表の名前らしきものが並んでおり具体的に見えますね。 しかし、いざこれをもとにデータを作ろうとしても、すんなりとはいきません。
どのデータ項目?
たとえば、「国勢調査 15歳以上非労働力人口」とは、正しくはどのデータのどの項目なのか。 これはまだ探しやすいほうですが、「事業所・企業統計調査 第2次産業事業所従業者数」とは、いったい何のどれなのか。 リンクはおろか表番号・項目番号の例示さえなく、専門家でもないかぎりピンときません。
メッシュ別生徒・学生数?
「通学地域メッシュ別生徒・学生数」に相当するものは、少なくとも公的な全国規模のオープンデータとしては存在せず、推計して求めねばなりません。 しかし、肝心のその推計方法がやはり漠然としています。
データを作る:基礎編
はじめに
長い前置きでしたが、ここからが本題です。 以上の状況を踏まえたうえで、昼間人口メッシュデータの自作に手探りで挑戦します。
以下その過程を、「令和2年国勢調査」の「3次メッシュ(JGD2011)」を基盤として説明します。 4次・5次メッシュも、参照するデータの表番号や項目番号が一部ずれるだけで作り方は同じです。
夜間人口
まずは基礎となる夜間人口のメッシュデータを作ります。 先の算出式を参考にいろいろと調べた結果、昼間人口との兼ね合いも考え、下記の3次メッシュ項目の合計を夜間人口としました。
なお項目名となっている用語の定義は、『国勢調査~ユーザーズガイド』で確認できます。 これに載っていない用語も、統計局のウェブサイトで探せばわかるでしょう。 これからさまざまな「人口」が登場するので、それぞれの意味や階層構造を覚えておくとはかどります。
- 労働力状態、産業分類及び職業分類別人口(15歳以上)(JGD2011)
- + 労働力人口 総数(T001189001)
- + 非労働力人口 総数(T001189010)
- 人口移動、就業状態等及び従業地・通学地(JGD2011)
- + 未就学者 総数(T001143019)
- + 在学者 総数(T001143034)
- - 当地に常住する15歳以上就業者・通学者 通学者数(T001143088)
非労働力人口とは、「15歳以上人口のうち労働力人口以外」と定義されています。 よって労働力人口と合わせれば、15歳以上のすべての人口を網羅できます。
残る15歳以下の人々は、未就学者と、義務教育の就学者(在学者総数から15歳以上通学者数を引く)と考えていいでしょう。 このデータの未就学者・就学者には「不詳」回答も含まれており、事情があって通学していない子なども入るようです。
これで夜間人口が求まりました。
……と、あっさり済ませるつもりだったのですが、結果が明らかにおかしい。 これらを合計してみると、113,680,000人しかいないのです。 総人口に1千万人ほども足りません。 誤差の範囲ではもちろんなく、何らかの「不詳」の影響にしては多すぎます。
「不詳」を甘くみるな
基礎でいきなり行き詰まってしまいました。 参照すべき項目が誤っているのでしょうか。 それとも、処理プログラムのバグでしょうか。
試しに労働力状態メッシュデータの合計値の内訳を出してみると、労働力人口は59,949,767人、非労働力人口は36,603,968人でした。
この数字を集計表と比べてみます。 『~労働力状態別人口及び労働力率(15歳以上)~』には、労働力人口59,949,767人、非労働力人口36,603,968人と書いてある。 ちゃんと合っていますね。
しかし表をさらによく見ると、端っこになんと、「労働力状態『不詳』」が11,704,834人もいるではありませんか。 これを合わせた数が15歳以上の本当の人口です。
さっき「『不詳』の影響にしては多すぎ」ると書きましたが、甘かった。 国勢調査の結果の実態は、実はこんな体たらくだったのです。
補完してみる
世も末ですが、この不詳人口はどう扱えばいいのでしょう。 安直に考えると、有効データに比例按分してしまえばよさそうですが。
こうした不詳の補完は調査統計における“通常業務”らしく、統計局はそつなくこなし、補完後の集計表も作っていました。 肝心の補完方法は、『令和2年及び平成27 年国勢調査に関する不詳補完結果(参考表)について』にありました。 主要項目による集計表を対象に、有効データの構成比に応じて不詳のデータを按分する、だそうです。 要するに、やっぱり比例按分でいいらしい。
基本的には、補完のための係数を「(不詳人口 + 労働力人口 + 非労働力人口)/(労働力人口 + 非労働力人口)」と求め、有効データに掛けていけばいいだけです。 人数なので、係数を掛けた結果は整数にします。
ただし、メッシュデータはふつうの集計表に比べて各項目(格子)の値が非常に小さく、単に係数を掛けただけでは正しく補完しきれません。 小数点以下の変化が整数化により切り捨てられてしまうためです。 たとえば、1に1.1を掛けても1のまま、4に1.1を掛けても4のままですね(四捨五入しなければ9に1.1を掛けても9のまま)。 こうしたいわゆる量子化誤差が大量に生じた結果、最終的な合計値はあるべき数字と隔たってしまいます。
そこで、簡単な誤差拡散法を取り入れます。 すなわち小数点以下の端数を、単に切り捨ててしまう代わりに、次に処理する格子の値に加算してやるのです。 統計学的な妥当性はさておき、効果はてきめんです。
まだおかしい
結果、夜間人口は計125,384,834人になりました。 それらしい数字ですが、正確な公表総人口126,146,099人にはまだ761,265人足りません。 1千万人に比べればだいぶ小さいとはいえ、引っかかる人数です。
15歳以下つまり就業状態メッシュのほうの合計値の内訳は、未就学者が6,123,667人、在学者が16,278,980人、マイナスする15歳以上通学者が5,276,382人。 これらにも「不詳」が絡んでいるのでしょうか。 しかし前に述べたように、未就学者・在学者にはもともと不詳が含まれているはず。
そして15歳以上通学者は、集計表『~常住地又は従業地・通学地別通学者数-全国~』の数字とちゃんと一致しています。 しかもたとえ在学者でも、「収入を伴う仕事を少しでもした人」は定義上通勤者扱いになるため、通学者はもともと事実より少なめに見積もられているはず。 よって、通学者の引き過ぎで76万人も足りないとは考えにくい。
そもそもおかしい
どうも変なので、試しに未就学者・在学者に卒業者数を加えてみると、計123,165,886人になりました。 そもそも総人口に300万人ほども足りませんね。 未就学者の定義は「在学したことのない人又は小学校を中途退学した人」、在学者は「在学中の人」、卒業者は「学校を卒業して在学していない人」で、論理的にはこれらを合わせれば総人口になるはずですが。
ひねくれた解釈ですが、中退者が卒業者に含まれていない可能性はあります。 ただ仮にそうだとしても、いま問題にしているのは15歳未満の人口です。 病気などによる休学者だって76万人もいないだろうし、まして少年院にもいるわけない。 ちなみに令和2年の小中学生の不登校児は約20万人で、これも関係なさそう。
もしや、在留外国人が含まれていないのか。 令和2年の外国人総数は(資料によって多少違うが)約275万人。 総人口の不足分にかなり近い。 が、15歳未満は約24万人しかいませんでした。 もとより就業状態データに外国人を除くなどとは書かれておらず(国勢調査は原則として外国人も含む)、やはり関係ないようです。
割り切る
いろいろ調べてみたものの、さっぱり原因がわかりません(もしかしたら、との心当たりはまだあるけれど証拠がない)。 統計局の算出式には、他に参照すべき表・項目はありません。 らちが明かないため、残念ながらこの件はここまで。 76万人は誤差として割り切ります。
残念ポイント 総人口が76万人少ない(原典の値が)
すっきりしませんが、それっぽいからこの項目を足せばいいか、などと素人料簡で無理にデータを“正す”わけにはいきません。 かえってデタラメになるだけです。 予測不能なデタラメさより、予測可能な誤差のほうがましでしょう。 一般にミクロな分析に用いられるメッシュデータにおいて、この程度のマクロな誤差はほとんど問題にならないはずです。
とはいえ実用性を考えると、最終的には公表総人口とのつじつまを合わせざるを得ないでしょう。 だとしても、今はこのまま話を進めます。 この記事が示す数字は、原則としてその時点での生の値です。
データを作る:推計編
昼間人口の基盤
いよいよ昼間人口に取りかかります。 第一段階として、夜間人口から流出人口を引いた昼間常住人口のメッシュデータを作ります。 やはり統計局の算出式を参考に、次の3次メッシュ項目を合計しました。
- 労働力状態、産業分類及び職業分類別人口(15歳以上)(JGD2011)
- + 非労働力人口 総数(T001189010)
- + 完全失業者 総数(T001189007)
- + 第1次産業 総数(T001189013)
- 人口移動、就業状態等及び従業地・通学地(JGD2011)
- + 未就学者 総数(T001143019)
- - 当地に常住する15歳以上就業者・通学者 通学者数(T001143088)
昼間人口において流出・流入するとみなされるのは、小学生以上の生徒・学生と、第2次・第3次産業の就業者です。 ここでは、それら以外の全人口を足しています。
一歩ずつ説明すると、まず始めに未就学者を置きます。 次に、「非労働力人口(15歳以上) - 15歳以上通学者」を加えます。 一見奇妙な式ですが、非労働力人口には生徒・学生も含まれるため、その分を引いているのです。 最後に、労働力人口から第2次・第3次産業就業者を除いた残り、完全失業者と第1次産業就業者を加えます。
労働力状態データのほうの各値には、忘れずに夜間人口のときと同じ不詳補完を施しておきます(係数を掛ける)。 結果、昼間常住人口の合計は46,675,465人になりました。
別の調査と結合する
第二段階、今度は流入人口を数えます。 確実なほうからいきましょう。 統計局の算出式に「事業所・企業統計調査」うんぬんとありましたが、あれはいったい何を指すのか。 結論をいうと、現在の「経済センサス」です。 あの算出式が書かれたあとに調査の名称変更(統廃合)があったようです。
経済センサスは国勢調査の法人版のようなもので、これも統計局が実施しています。 事業所の場所や業種、そこで働く従業者数などがメッシュデータとして公開されており、流入人口の算出にうってつけ。 共通の地域メッシュコードをキーにして、国勢調査メッシュと簡単に結合できます。
ただし、あくまでも国勢調査とは別の調査であることに注意。 調査の仕方も対象も違えば、何より実施時期も違います。 当然、国勢調査の就業者数と経済センサスの従業者数とは整合しません。 それでもほかにデータがない以上、不整合は誤差と割り切りこれを使うしかありません。 統計局のかつての推計も同様だったので、その旨さえ明示すればかまわないでしょう。
注意ポイント 異なる種類・年度の調査結果が混ざる(必然的に)
というわけで、「令和3年」の「経済センサス」より、次の3次メッシュ項目を昼間人口に加えます。
- 産業(中分類)別事業所数及び従業者数(JGD2011)
- + 従業者数:A~S全産業(T001158108)
この項目の合計は62,427,908人でした。 これも最終的には令和2年の公表総人口とのつじつまを合わせますが、今はこのまま進めます。
生徒・学生数を調べる
統計局を参考に
第三段階、最後にして正念場です。 生徒・学生の流入人口の推計方法をひねり出さねばなりません。 統計局の推計方法を確認します。
通学地域メッシュ別生徒・学生数は、平成13年事業所・企業統計調査の対象事業所から学校を抽出し、学校基本調査等に基づいて生徒・学生数を把握し、平成13年事業所・企業統計調査に関する地域メッシュ統計(世界測地系)の編成における各学校の地域メッシュに対応付け、地域メッシュ別に集計しました。
(『平成12年国勢調査,平成13年事業所・企業統計調査等のリンクによる地域メッシュ統計』より)
わかりにくいですが要するに、経済センサスのメッシュデータから学校を見つけ、「学校基本調査」を利用してそこの生徒・学生数を割り出せばいいらしい。 それ以上具体的なことは書かれていません。
経済センサスのメッシュには、「中分類」には「学校教育」の、「小分類」にはさらに細かく「中学校」や「高等教育機関」などに分類される事業所数・従業者数が含まれています。 こうした事業所をすなわち学校とみなせばいいようですね。
いっぽう学校基本調査とは、文部科学省が実施する一斉調査で、全国の学校のさまざまな統計を毎年度公表しています。 ただしあくまでも統計であって、各校の生徒・学生数を個別に網羅するデータは公表されていません。 ざっと見て経済センサスと組み合わせて使えそうなのは、学校分類×都道府県別の生徒・学生数の集計です。
推計方法
これらの情報を使ってできそうなのは、次のような推計です。
経済センサスメッシュの格子から学校に相当する事業所を見つけ、その学校分類と当該格子の都道府県(「市区町村別メッシュ・コード一覧」参照)とを得、対応する生徒・学生総数を学校基本調査に求め、按分する。
按分の方法は、その学校の従業者数に応じた比例按分にしてみます。 「ある学校の生徒・学生数は、その学校の従業者数に比例する」と仮定するわけです。
この仮定は明確な根拠こそないものの(法令で最低限度くらいは定めてるかも)、不合理でもないはずです。 「教員ひとりあたりの生徒数」はよく聞く指標だし、この規模の学校ならこれくらいの教職員数、との経済的・経験則的な合意はわれわれの間にもあるでしょう。
データの整理
学校基本調査
推計方法が固まったので、用いるデータを具体的に整理します。
学校基本調査の統計は学校分類ごとまとめられており、その中に生徒・学生数を都道府県別に集計した表があります。
大学と短期大学の表には、都道府県だけでなく都市別の学生総数が一部「再掲」されていますが、精度向上のためちゃんと処理に反映させます。 以下いちいち書きませんが、大学・短大を扱う際には、都道府県の種類に再掲都市も含まれると考えてください(47都道府県+21都市)。
ところで、学校基本調査の年度は国勢調査と経済センサスのどちらに合わせるべきでしょうか。 統計局の説明はあいまいです。 ここでは、計算上の結びつきの強い経済センサスとの整合性を重視し、「令和3年度」の表を参照することにしました。
経済センサス
経済センサスメッシュには、学校の事業所・従業者数を分類ごとに示す次の項目があります。
- 産業(小分類)別事業所数及び従業者数(JGD2011)
- 事業所
- 812 小学校(T001159038)
- 813 中学校(T001159039)
- 814 高等学校,中等教育学校(T001159040)
- 815 特別支援学校(T001159041)
- 816 高等教育機関(T001159042)
- 817 専修学校,各種学校(T001159043)
- 従業者
- 812 小学校(T001159182)
- 813 中学校(T001159185)
- 814 高等学校,中等教育学校(T001159188)
- 815 特別支援学校(T001159191)
- 816 高等教育機関(T001159194)
- 817 専修学校,各種学校(T001159197)
- 事業所
こちらには義務教育学校(比較的新しい小中一貫校)の項目がないため、学校基本調査の義務教育学校の生徒総数は、6:3の割合で小学校・中学校に按分することにします。
事業所と従業者との関係には注意を要します。 学校従業者のいるところには必ず学校事業所があるようですが、学校事業所のあるところに必ず学校従業者がいるとは限りません。
ふだん無人の学校関連施設はいくつか思いつくとはいえ、経済センサスへの回答として、均等割を払っているような「事業所」に従業者がいないことなどあるのでしょうか。 調べてみると、法的にはあり得るようです。 他方、単なる回答不備の可能性も否定できません。
迷いましたが、ここでは余計な解釈をせず、額面通りゼロ人と受け取ることにしました。 したがって推計においては、たとえ学校の事業所があっても、そこの従業者数がゼロなら生徒・学生数もゼロになります。 いずれにせよ、そんな事業所は全国に数えるほどしかなく、大勢には影響ないでしょう。
処理手順
以上、これらのデータを組み合わせて処理すれば、メッシュデータ上の学校の生徒・学生数を推計できます。具体な手順は次のようになります(数字はすべて仮)。
- 事前計算
- 比例按分の分母とするため、学校分類×都道府県ごとの学校従業者の総数を、「産業(小分類)別事業所数及び従業者数」メッシュから求めておく
- 本計算
- 「産業(小分類)別事業所数及び従業者数」メッシュの格子を走査する
- ある格子に、「小学校の従業者」が40人いた
- 「市区町村別メッシュ・コード一覧」より、当該格子は「X県」に属する
- 事前計算より、X県の小学校の従業者総数は計20,000人である
- 「学校基本調査」より、X県の小学校の生徒総数は300,000人である
- この格子には、40 ÷ 20,000 × 300,000 = 600人の生徒がいる
大学の従業者とは?
これでようやく生徒・学生の流入人口が求まります。 と思いきや、おかしなことに気づきました。 従業者数の異常に多い高等教育機関があるのです。 このまま学生総数を比例按分してよいものか。
いくつか抽出して調べてみると、異常なのはいずれも大学のようです。 「生徒・学生数は学校の従業者数に比例する」との仮定を述べましたが、高等教育機関、とりわけ大学では事情が少々異なります。 とは知りつつも、少々異なりはするけれどそう極端には違わないはず、との仮定でいっしょくたに処理していました。 ところが事実は、思いのほか極端に違っていたのです。
1校(正確には1格子)あたりの従業者数は次のとおりでした。
| 分類 | 最小 | 中央 | 最大 | 平均 | |
|---|---|---|---|---|---|
| 小学校 | 1 | 27 | 312 | 32.5 | |
| 中学校 | 1 | 31 | 295 | 33.6 | |
| 高等学校,中等教育学校 | 1 | 70 | 602 | 77.9 | |
| 特別支援学校 | 1 | 89 | 410 | 97.9 | |
| 高等教育機関 | 1 | 152 | 10,650 | 355.7 | |
| 専修学校,各種学校 | 1 | 22 | 1,304 | 47.9 |
教員の業務形態の違いもさることながら、問題は職員のようです。 横にも縦にも広い町のような敷地のさまざまな施設で働く、パートタイムも含む職員すべてを集めたらえらい数になるわけですね。 中でもおびただしいのは大学病院です。
世間知らずなもので調べて驚きましたが、大学病院に専任で働いている人も、大学に雇われている以上肩書は大学職員らしいのです(本当?)。 うちの地元にも巨大な大学病院がありますが、あそこの職員の多くが大学職員だとしたら、確かにべらぼうです。
それにしても最大1万人越えとは、実際の内訳はどうなっているのでしょう。 1人しかいないところも気になりますが。
調整
正体が何であれ、こうした過剰な従業者数はさすがに学生数を反映しないと考えられるため、対策せねばなりません。
いろいろ考えたり試したりしたあげく、比例按分を計算する際、対象の従業者数を「1,000を上限に丸める」ことにしました。 ある学校の従業者数が5,000だろうが10,000だろうが、1,000とみなして按分するわけです。 1,000以下ならそのまま。
この方法や1,000という数に根拠はありません。 いかにも乱暴なのは承知ですが、最も単純でわかりやすいのでこうしました。
反対にやりたくなかったのは、下手な関数をでっちあげること。 統計学のエキスパートが他の関連情報をも駆使して練り上げるならともかく、素人が思いつきで急造してみたところで結局デタラメなうえ、やはり予測不能に陥ってしまいます。 いずれにしても、しょせんは間接的な情報による、あいまいな仮定の上の推計にすぎません。 あまりこだわっても仕方ないでしょう。
警告ポイント 生徒・学生数の見積もりが怪しい(推計の限界)
エンディング
仕上げ
そもそも夜間人口が公表総人口に満たない、出典の調査・年度の違いから昼間人口と夜間人口が一致しない、といった問題点を述べました。 結局、生のデータの内訳は次のようになりました。
| 項目 | 合計 | データ出典 |
|---|---|---|
| 昼間:常住 | 46,675,465 | R2国勢調査 |
| 昼間:通勤 | 62,427,908 | R3経済センサス |
| 昼間:通学 | 16,500,578 | R3経済センサスとR3学校基本調査による推計 |
| 昼間人口 計 | 125,603,951 | ― |
| 夜間人口 | 125,384,834 | R2国勢調査 |
| 昼夜差分 | 219,117 | ― |
正直な値ではあるものの、このままでは全体の昼夜間人口比率が100ちょうどにならないなど、一般的な用途に使いにくそうです。 そこで最後に、次の手順でストレッチしてこうした差異を解消します。
- 「(夜間人口 - 昼間:常住)÷(昼間:通勤 + 昼間:通学)」を昼間:通勤と昼間:通学に掛け、昼間人口を夜間人口にそろえる。
- 「公表総人口126,146,099 ÷ 夜間人口」をすべての項目に掛ける。
この加工後の最終的なデータの内訳は次のとおりです。
| 項目 | 合計 | データ出典 |
|---|---|---|
| 昼間:常住 | 46,958,852 | R2国勢調査(加工済) |
| 昼間:通勤 | 62,632,573 | R3経済センサス(加工済) |
| 昼間:通学 | 16,554,674 | R3経済センサスとR3学校基本調査による推計(加工済) |
| 昼間人口 計 | 126,146,099 | ― |
| 夜間人口 | 126,146,099 | R2国勢調査(加工済) |
| 昼夜差分 | 0 | ― |
メッシュの区分
3次メッシュだけでなく、4次・5次メッシュも作りました。 原則として同じ区分(4次なら4次、5次なら5次)の統計メッシュデータを原典とします。 ただし、経済センサスには5次メッシュが存在しないため、4次メッシュを2×2マスに按分して国勢調査の5次メッシュと結合しました。
完成!
さんざん試行錯誤しましたが、とにかくやっとできました。 全国合一のCSVファイルとし、3~5次をまとめてZIPアーカイブしました。 冒頭のリンクボタンでダウンロードできます。
使用許諾(ライセンス)
この昼間人口メッシュデータ(以下、当データ)は、データの出典元である「政府統計の総合窓口(e-Stat)」の利用規約を継承し、それと互換性のある「クリエイティブ・コモンズ・ライセンス 表示 4.0 国際(CC BY 4.0 )」に従って使用できるものとします。
改変点の表示
当データは、「政府統計の総合窓口(e-Stat)」提供の原典を、「はんけトケ」が利用・加工して作成したものです。
当データは、上述のとおり妥協含みの推計です。 「政府による信頼性の高い実測データだ」などとエンドユーザーが誤解しないよう、第三者による加工データである旨を明記してください。
免責について
原典データの提供者および当データの加工・作成者は、利用者が当データを用いて行う一切の行為(データを編集・加工等した情報を利用することを含む)について何ら責任を負うものではありません。
推計の精度は?
ところで、このデータの精度・正確性はどれくらいでしょうか。 推計データには、正となる比較対象データがない、との宿命があります。 もし正のデータがあるなら、そもそも推計する必要がないからです。
そこで代わりに、このデータのメッシュ上の昼間・夜間人口を市区町村ごとに集計し、国勢調査の市区町村別昼間・夜間人口データと比べてみます。 これは令和2年国勢調査の「従業地または通学地」回答をまとめたもので、翌年の経済センサス・学校基本調査の数字とはもとより一致しませんが、目安にはなるでしょう。
両者の昼夜間人口比率を、「推計データの昼夜間人口比率 ÷ 国勢調査の昼夜間人口比率」の式で比べてみます。 ぴったり一致すれば1.0、倍多すぎたら2.0、のような値になるわけです。 全市区町村(不明を除く)のこの値をまとめた結果は次のとおり。
| 最小 | 中央 | 最大 | 平均 | 標準偏差 | 1.0からの偏差 | |
|---|---|---|---|---|---|---|
| 0.0778 | 0.9976 | 5.0458 | 1.0234 | 0.1939 | 0.1953 |
中央値・平均値は1.0に近いですね。 そこそこバラつき(偏差)があるのは、「もとより一致しない」うえに推計が混ざるのだから仕方ないでしょう。 もしバラつかなかったら、奇跡かインチキかバグです。
とはいえちょっと振れが大きいでしょうか。 最小値・最大値の異常さも気になります。
異常値については、推計方法が完璧からほど遠い以上、中にはそんな値も出ることだろうと思います。 振れの大きさについては、当該市区町村の人口の少なさも原因のひとつと考えられます。 分母となる人口が少ないほど、誤差が大きく影響するわけです。
試しに、昼間人口を縦軸(対数であることに注意)にとったグラフに値をプロットしてみました。
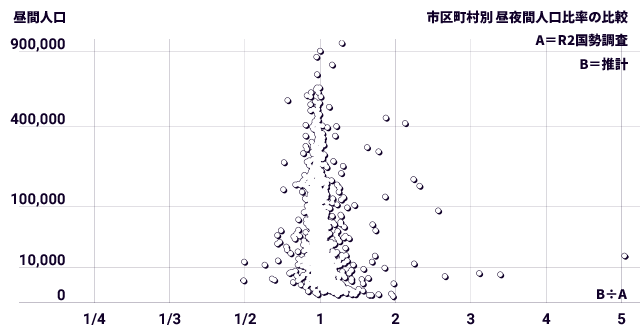
おおむね予想どおり、人口が少ないほど振れが大きくなる傾向があり、そして外れ値といえる点がちらほら出ていました。 ついでに明らかになったのは、少なすぎより多すぎの点が多いこと。 ともあれ最頻値がちゃんと1.0辺りで、対象市区町村1,887件のうち外れがこの程度なら、原典の違いも考慮すればまずまず健闘しています。 この比較の結果表(CSV形式)も参考にしてください。
推計を抜くと?
では、メッシュの昼間人口から通学者を抜いたら、つまり生徒・学生数の推計を抜いたら結果はどう変わるでしょうか。 国勢調査と経済センサスの実測値を素直に足した数になるのだから、バラつきや外れがずっと減ると予想されます。
通学者抜きメッシュで同じ比較をしてみた結果は次のとおり。
| 最小 | 中央 | 最大 | 平均 | 標準偏差 | 1.0からの偏差 | |
|---|---|---|---|---|---|---|
| 0.0778 | 0.8709 | 5.0458 | 0.8817 | 0.1708 | 0.2078 |
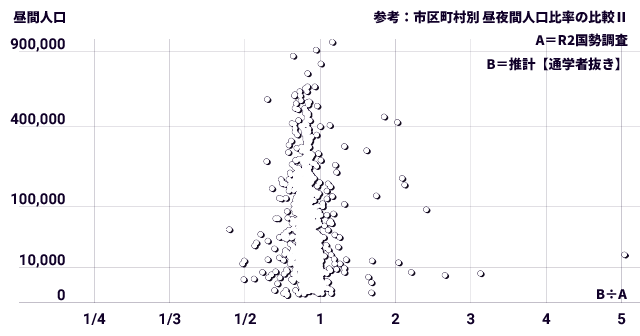
意外な結果が出てしまいました。 中央値・平均値が1.0より明らかに少ない(グラフが全体に左に寄る)のは通学者を抜いたぶん数が足りないので当然として、問題はバラつきが大して変わらないことと、何より外れ値です。 極端な外れが生じるのは推計のせいと思いきや、実は関係なかったのです。
確かに考えてみれば、人口に占める通学者の割合は少ないのだから、それが結果を大きく左右するのは不自然といえます。 とにかく元がこれでは、推計式をいくらいじっても焼け石に水。 むしろ、通学者を足すことでグラフがほぼ形を変えず真ん中にそろうということは、推計式はあれで案外穏当なのかもしれません。
諸々補正しない国勢調査・経済センサスメッシュの原数値を使っても、グラフの形はほぼ同じでした。 つまり、データ作成過程で値が狂ったわけではありません、念のため。
この結果をどう評価するか(そもそもこの比較に意味があるのか)、この昼間人口データが実用に足るかどうかの判断は、目的にもよるため利用者に委ねます。
奇怪ポイント 市区町村別昼間人口と一部大差がある(推計によらず)
ついでに示しておくと、通勤者も抜くと次のグラフになります。
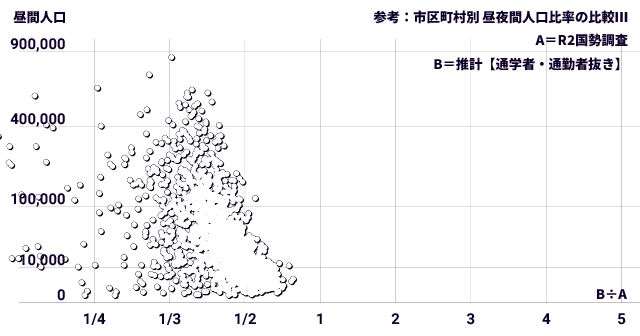
おわりに
推計昼間人口メッシュデータを自作し、なおかつこうして公開したのは、直近の国勢調査等に基づくオープンで全国規模の昼間人口メッシュデータが、その有用性と根強い需要とにもかかわらず存在しないことに疑問を覚えたためです。
ならば自分が統計局代わりに立ち上がろう、などと気負ったわけではありません。 この記事を読めばわかるように、そんな知見は持ち合わせていません。 ただ、わたしのように多少不正確でも昼間人口メッシュを使ってみたい、知見はなくても昼間人口メッシュを作ってみたい人たちのための、たたき台があるとよいと思ったのです。
半端な品質なのに公開しているのも、大半の人は関知しないであろう詳細を長々記したのもそのためです。 たとえ半端でもデータとそのレシピがあれば、使ってみたけどここが変だ、それはあそこが間違ってるからだ、と議論できます。 しかし、何もなければ始まりません。
統計局がまた昼間人口メッシュを作って公開してくれれば、このデータは不要になります。 そうなることを望みますが、だとしても、わたしたち市民が自ら推計し比較・検証できる道を開くことには、少しは意味があるでしょう。
用語・注釈
- 流出・流入人口について
- 転居を意味する「転出・転入人口」と混同しないように。
- 昼間・夜間人口について
- 紛らわしいがこれらは便宜上の呼び方で、流入・流出の実際の時間帯は問題にしない。 夜学や夜勤も昼間人口に含まれる。
- 商圏分析
- 商いやすい出店場所をデータに基づいて検討すること。
- 地域メッシュ
- 政府の定めたメッシュ体系(JIS X 0410)。 メッシュ上の各格子は、経緯度と相互に変換できる一意の番号「地域メッシュコード」を持つ。
- 按分
- 値をある基準で複数の対象へ分けること。
- 不詳補完について
- そもそも補完済みのメッシュデータを公開してほしい。 按分ではないより高度な補完法を統計局は研究中らしいが、それが主流になったら真似もしにくくなる。
- 予測可能
- 因果関係が明瞭なこと。
- 昼夜間人口比率
- 文字どおり昼間人口と夜間人口の比。「100 × 昼間人口 ÷ 夜間人口」で求める。
補遺
些末なわりに長くなるため本文に書かなかった事柄などを補足します。
大学・短期大学の「再掲」
集計表を読めば察しがつくため本文では軽く流しましたが、大学・短大の「再掲」とは具体的にどういうことでしょうか。
たとえば仮に、A県に大学生が10万人いる、と集計表に書かれているとします。 そしてさらに、「再掲」としてA県の政令指定都市B市に大学生が7万人いる、と書いてある。
この意味は、A県のB市に大学生が7万人おり、B市以外の残りに大学生が3万人いる、ということです。
これに応じてプログラムでは、都道府県とこうした再掲都市とを同列に扱い、A県の大学生は3万人、B市の大学生は7万人、との情報を持ちます。 そしてメッシュの行政区を判定する(市区町村コードを求める)際には、都道府県と再掲都市とを区別します。 こうすれば、学生数の按分に「再掲」の別を反映できるわけです。
ただしこれは、やや単純化した説明です。 再掲都市は、たとえば東京23区のように複数の区を含んでいたりするため、それらをまとめて扱う必要があります。
それと実際の按分処理では、経済センサス側の分類に合わせ、大学・短大・高専を「高等教育機関」として合算して扱います。 大学と短大とは同じ都市が再掲されているため、その区別ごと合算すればいいだけです。 しかし高専には再掲がないため、適当に按分することになります。
ところで高専は、各都道府県に1校あるかないかくらいなので、再掲都市の内にあるか外にあるか個別に調べ、按分ではなくどちらかに値を振るべきとも考えられるかもしれません。 しかし裏を返せば、1校あるかないかの学生数ならそこまでせずとも大勢に影響ありません。 きりがなく線引きもあいまいなため、高専に限らずたとえ可能そうでも学校個別の調査は控えます。
「市区町村別メッシュ・コード」の適用
重複の問題
「市区町村別メッシュ・コード一覧」を利用して地域メッシュコードに対応する市区町村コードを求める際、まずひとつ問題がありました。 「市区町村別メッシュ・コード一覧」表は都道府県別のファイルですが、各都道府県の境界に相当するメッシュに一部重なるところがあるのです。
たとえばA県とB県の県境のメッシュが重なったら、どちらの県とすべきでしょうか。 特に気にせず処理すると、北海道から沖縄まで都道府県順の若いほう(あるいは古いほう)が結果的に選ばれると思います。
それはそれで一貫性があるとはいえ、必然性も保証もなく気持ちが悪いため、とりあえず「人口の多い都道府県を優先する」ことにしました。 厳密にいえば流動的で、あまりうまい手ではありませんが。
もし正解があるとすれば、都道府県境のデータとメッシュとを突き合わせ、どちらの県がより多くの面積を占めるか調べればいいのでしょう。 が、ちょうどそんな境界上に学校でもないかぎり実質的な意味はなく、あったとしても大勢に影響せず、面倒なので見送りました。
粒度の問題
これも境界に関することですが、もうひとつ根本的な問題があります。 「市区町村別メッシュ・コード一覧」が3次メッシュであることです(どうせ作るならもっと細かくしてくれればいいのに……)。
3次メッシュはおおよそ1キロメートル四方の格子です。 市区町村の境を分けるにはやや大雑把にすぎ、本当はA市にある学校をB市にあると誤判定しかねません。 市区町村単位での人口集計にも影響し、これは試しておらず憶測ですが、精度判定の外れ値はこれが原因している可能性もあります。
境界ポリゴン情報などを利用し、アナログ的あるいは少なくとも5次メッシュ相当の粒度で境界を区別すべきかもしれません。 しかし、やはり前節と同じ理由で見送りました。
4次から5次への按分
5次メッシュデータを作る際、経済センサスのメッシュは4次までしかないため、2×2マス(=4マス)に按分して5次の代用とすることは述べました。
そのように人口つまり整数を按分する際、4で割り切れない余りは、各マスに1人ずつ振り分けることになります。 このとき、たとえば2人余ったとして、2×2のどのマスに振り分けるべきでしょうか。
特に考えなければ、素直に地域メッシュの分割コード順になるでしょう。 すなわち、左下・右下・左上・右上の順。 しかしこの順番で2人を振り分けると、下方に人が偏ってしまいます。
これを避けるため、振り分けの順番を、左下・右上・右下・左上とすることにしました。 実際には4人余ることはないため、左上は使われません。
この振り分け方でも結局偏りはするものの(しま模様で考えると水平線が斜線になるだけ)、マス同士の距離でいえばより分散したことにはなるでしょう(1 → √2)。
ちなみに、本当に偏りをなくしたければランダムに振り分ける手がありますが、再現性に難があります。 代わりにランダム風のパターンを使う手も、恣意的なパターンに依存する点でやはり恒久的な再現性に難があります。
ついでに書いておくと、この按分では地形は考慮されません。 つまり、たとえばちょうど海岸線をまたぐメッシュを2×2マスに割ったとき、どれかのマスは完全に海の上に位置するかもしれません。 これを避けるには別途地形データを参照せねばなりませんが、そこまでこだわる意味があるとは思えず見送りました。
誤差拡散法の始末
メッシュに対する計算に簡単な誤差拡散法を使いました。 量子化誤差を解消する(ごまかす)便利な手法ですが、ときにより最後に値が1不足することがあります。 たとえば、ある人口の合計は10,000になるはずなのに、9,999になってしまうなど。
この不足の1は、最後に余った「誤差」の中に残っているのです。 それを四捨五入すると1になるはずです。
もしこのように1余ったら、計算対象のうち値が最大の(1くらい増えても影響が少ない)ところに足すことにしました。
生徒・学生数のヒント
生徒・学生数の推計方法はデータの精度を左右する鍵ですが、もっと改善する方法はないでしょうか。 統計局の推計方法をもういちど確認します。
〜事業所から学校を抽出し、学校基本調査等に基づいて生徒・学生数を把握し、〜
「等」が意味深長です。 学校基本調査の他にも手がかりがあったように読めますね。 それが何だったかは例によって不明なのでさておいて、補助線となり得る関連情報がないか自分でも探ってみます。
市区町村別昼間・夜間データ
本文の最後に、国勢調査の市区町村別昼間・夜間データとの比較をしました。 精度を上げるには、ああしたグラフとにらめっこしながら式の変数を調整し、推計結果を市区町村データに近づけていけばいいのでしょうか。
いや、そんな回りくどいことをしなくても、市区町村データを推計処理に組み込んでしまえばいいのです。 つまりたとえば、生徒・学生数を学校に按分するとき、その学校が属する市区町村の昼間人口を超えないように調整するとか。
ひとつの市区町村に同じ分類の学校がよほど集中していないかぎり、従業者数による比例按分なんぞしなくても、この方法だけでずっと本当らしい結果を得られるような気がします。
ただ、よくよく考えてみると計算が大変ややこしい。 学校には(すなわち生徒・学生にも)分類があり、そのどれを含むかは市区町村ごとに異なり、このまだら模様は一筋縄で処理できないのです。
それにそもそも、昼間人口を推計するのに他の昼間人口データにそこまで大きく頼るのは、予定調和というか本末転倒というか、ならば単に市区町村データの昼間人口をメッシュに按分してしまうのとどう違うのか、との疑問も生じます。 もっとも、実用になりさえすれば作り方なんてどうでもいいのも確かですが。
学校コード表
文部科学省の「学校コード」の表は、全国の学校のコード・校名だけでなく、分類や住所をも網羅した有用なデータです。 生徒・学生数が含まれないのが惜しいものの(それさえあれば推計する必要もない)、毎年度の履歴もちゃんとあり、他の調査との相性もよさそうです。
生徒・学生数を推計するうえでまずあいまいだったのは、学校を経済センサスの事業所・従業者数から割り出していたこと。 それが本当に学び舎か、漏れがないか、確信を持てませんでした。
しかし、この学校コード表を正として突き合わせればはっきりします。
ただし、この表をメッシュと突合するには、表内の全住所を経緯度に変換(ジオコーディング。APIで自動化できるとはいえ、結果に間違いないか確認を要する。逆変換してみたり、多種のAPIの結果を比べてみたり、地図を目視してみたり)し、さらに経緯度を地域メッシュコードに変換したうえで、多少の幅を持たせて一致判定せねばなりません。
そうまでがんばったところで修正される正誤が果たしていくつあるか考えると、費用対効果が疑われて結局利用を見送りました。 が、強力なヒントであることは確かです。 いつか使う機会があるかもしれません。
【追記】 学校の経緯度については、国土数値情報の「学校データ」に網羅されているようです。 毎年度更新ではありませんが、不足分くらいは手作業で補えばいいでしょう。
市販の学校データベース
市販の学校データベースを購入する手もありますが、そんなお金があるなら市販の昼間人口メッシュデータを買ったほうが早い。 それにもし市販のデータを使ったら、ライセンス上その二次加工データを公開することが難しくなってしまいます。
自分で調べる
学校によっては、生徒・学生数をウェブサイトに掲載しています。 こうした情報を自前で適当な数集め、標本として推計に利用する手があります。 学校情報の収集に特化したウェブクローラーをこしらえてしばらく泳がせてみてもいいかもしれません(教育機関は独特のドメイン名を持っており絞り込みやすい)。 ただ、過去の履歴まで丁寧に載せているところは少ないでしょう。
知識
そもそも本来、対象領域(この場合は学校の運営・経営・制度等)を学びもせずに仮定・推計などするものではありません。 にもかかわらず下手にするから、極端な従業者数に直面してあわてたりするわけです。
つまり学校そのものについての知識こそが、最も基本的かつ有効な手がかりであるといえるでしょう。 極めれば、明文化されたデータのみならず、立地や地方の特色といった暗黙の地理条件をも加味して生徒・学生数を見積もれるかもしれません。
とはいえ、これこそ最も時間も労力もかかる方法であり、昼間人口を求めるだけのためにそこまでするか、という話ではあります。
過去のデータ
平成27年国勢調査や、さらに過去へさかのぼって同様の昼間人口メッシュデータを作ることができないか。 端的にいえば、できません。
具体的にいえば、原典となるメッシュデータが足りず(少なくともウェブ上に公開されておらず)、作るのが難しいのです。 もし強いて作ろうとすれば、方法をわりと根本から見直さねばならないうえ、生徒・学生数の推計がもっとずっとあいまいになってしまいます。 面倒くさくて空しいですね。
ちなみに未来についても同じことで、オープンデータ化の理念や技術が後退するとはまさか考えにくいものの、今回と同等以上の原典がもし公開されなかったらお手上げです。
開発について
参考のため、この昼間人口データを作るためのプログラムについても触れておきます。
開発言語はCSVファイルを、つまりテキストと配列さえ簡単に扱えれば何でもかまいません。 スマートに高速に処理する必要などなく、自分がラクに書ければいいのです。 どうせ今どきのコンピューターは、どんなに雑なプログラムでもCSVのメッシュデータごとき瞬く間に処理します。 わたしは基本的にPHPを使いました。
昼間人口の推計は複数のデータが絡んで相当ややこしく見えますが、一歩々々は単純なロジックです。 なので、「step1.php」「step2.php」のようにプログラムを分け、本当に一歩ずつ処理しました。
メッシュCSVを読み、一歩だけ加工処理し、CSVとして出力する。 そのCSVを読み、一歩だけ加工処理し、またCSVを出力する。 との具合にバトンを渡していったのです。 すべて出来上がったらバッチ実行すればいいわけです。
この原始的な方法には、各段階が独立している見通しの良さに加え、途中経過がCSVとして目に見えるため検証やデバッグをしやすい、処理を毎度いちから繰り返さずに済み試行錯誤がはかどる、といった利点がありました。
メッシュの区分(3〜5次)は簡単に環境変数で指示しました。 区分によって原典のファイル名や項目番号が異なったり、地域メッシュコードの桁数が変わったりするので、柔軟に、ではなく泥臭く場合分けで対処しました。 5年に一度(国勢調査の周期)しか使わぬようなプログラムを丁寧に作っても仕方ありません。
5年周期といえば、問題は文書化です。 昨日食べたものさえ覚えていないのに、こんなプログラムの内容を5年後に覚えていてつつがなく再実行、必要に応じて修正等々できるはずがありません。 少なくとも備忘録が要ると思い、この記事は半ばそのつもりで書きました。
(最終更新:2026.1.3)